Spiegelbild Spiegelparadoxon

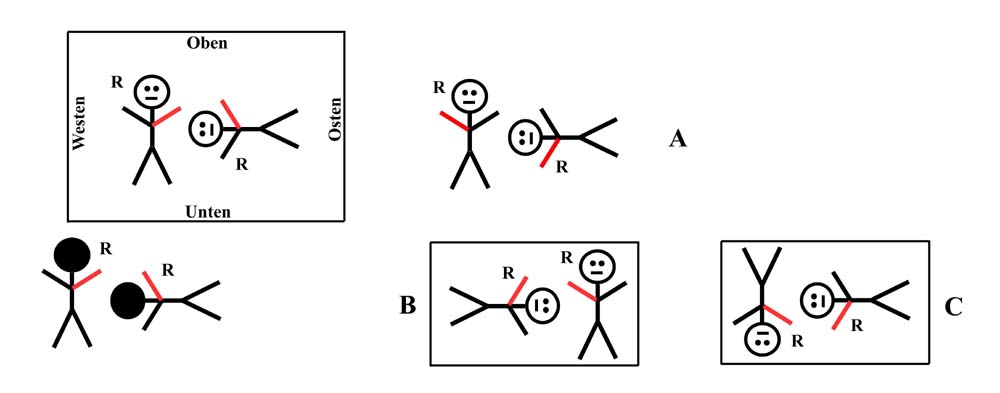
Warum sehen wir im Spiegel alles „spiegelbildlich“?

Warum sieht man in einem Spiegel links und rechts seitenverkehrt aber nicht oben und unten?

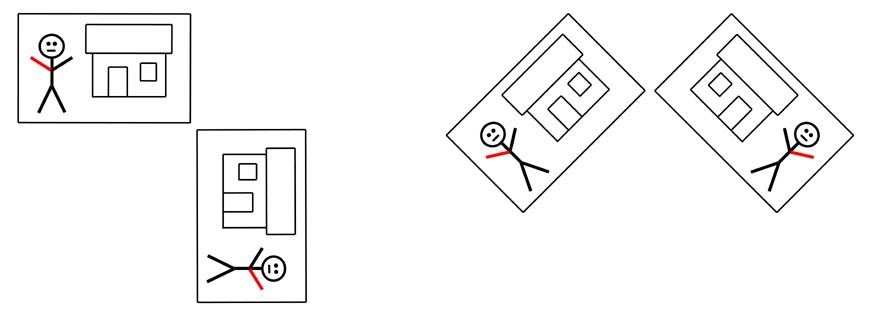
Nun, wie man im folgenden Bild sieht ist der Westen und Osten eines Spiegelbildes genau so wenig vertauscht wie Oben und Unten in einem Spiegelbild vertauscht sind. Dagegen ist aber Oben und Unten in einem Spiegelbild im Sinne von links-rechts genau so seitenverkehrt wie der Westen und Osten dieses Spiegelbildes im Sinne von links-rechts seitenverkehrt ist.
Das liegende Männchen erscheint im Spiegelbild genau so links-rechts seitenverkehrt wie das stehende. Für das liegende Männchen ist der Fußboden links und die Zimmerdecke rechts, im Spiegelbild ist es umgekehrt, gerade so wie die Zimmerwände für das stehende Männchen im Spiegelbild seitenverkehrt sind. Aus Sicht des stehenden Männchens hat das liegende Männchen seinen Kopf links, im Spiegel ist es umgekehrt. Aus Sicht des liegenden Männchens hat das stehende Männchen seinen Kopf rechts, im Spiegel ist es umgekehrt.

Bild 1

Allerdings beobachten wir normalerweise nur an einzelnen Objekten bzw. an uns selbst dass wir im Spiegelbild seitenverkehrt erscheinen, meist aber nicht an unserer Umgebung.

Dass wir an den beiden Männchen im Bild vorher registrieren, dass sie seitenverkehrt im Spiegelbild sind, liegt daran, dass sich Männchen, die uns aus der Richtung des Spiegelbildes entgegen sehen wollten, sich dazu ja um eine Achse um 180 Grad drehen müssten wie es rechts neben dem Spiegelbild (A) dargestellt ist. Beim Drehen eines Objekts um eine Achse (z.B. oben-unten) werden ja zwangsläufig die beiden anderen Achsen um 180 Grad gedreht d.h. die beiden anderen Richtungen (vorne-hinten, links-rechts) werden vertauscht. Im Spiegel wird aber, durch die Umkehrung der Lichtstrahlen, nur eine Richtung vertauscht, nämlich vorne und hinten. Die drei Achsrichtungen des Spiegelbildes passen sozusagen nicht mehr zusammen. Dies ist im Prinzip der Grund dafür dass das Spiegelbild spiegelbildlich bzw. seitenverkehrt ist. In einem Spiegelbild wird das Licht immer am gleichen Ort reflektiert, Osten bleibt Osten, Westen bleibt Westen, Oben bleibt Oben und Unten bleibt Unten, nur die Richtung normal auf den Spiegel, also vorne und hinten wird umgedreht.
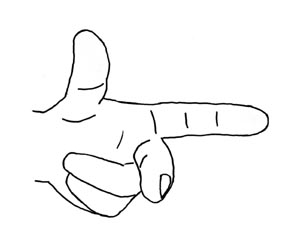
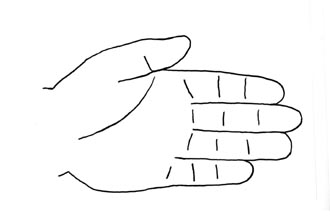
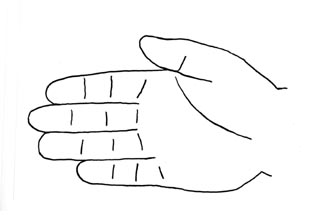
Bei einem zweidimensionalen Bild wird Vorderseite mit Rückseite vertauscht, denn auch ein Bild muss man ja um eine Achse drehen damit man es aus der Richtung sieht aus der man das Bild im Spiegel sieht. Man kann es sich auch damit veranschaulichen dass man eine Hand mit der Handfläche zum Spiegel hält. Will man die Handfläche direkt sehen will so muss man ja die Hand um eine Achse um 180 Grad zurück drehen womit auch links und rechts der Hand vertauscht wird.

Dass im Spiegel faktisch vorne (Vorderseite) mit hinten vertauscht wird, in der Ebene des Spiegels aber alles dort bleibt wo es ist, also keine zweite Richtung vertauscht wird, ist also im Prinzip der Grund dafür dass das Spiegelbild seitenverkehrt ist.

Was wir allerdings nicht registrieren ist, dass das Spiegelbild ja als Ganzes seitenverkehrt ist. Wenn man nämlich von den beiden Männchen von vorne ein Foto machen wollte und es um die senkrechte Achse um 180 Grad dreht, so sieht das Bild der beiden Männchen so aus wie es im obigen Bild Mitte (B) dargestellt ist. Nicht die beiden Männchen für sich sind seitenverkehrt im Spiegel sondern das Spiegelbild als Ganzes ist seitenverkehrt. Aber auch gegenüber diesem gesamten Bild sind beide Männchen im Spiegel seitenverkehrt.

Dies ist nun aber ein interessanter Effekt. Denn wir beobachten wohl an einzelnen Objekten, bei denen links und rechts definierbar ist, also etwa unser Gesicht, dass sie im Spiegelbild seitenverkehrt sind, wir registrieren aber nicht dass in Wirklichkeit das ganze Bild, also auch unsere Umgebung im Spiegel seitenverkehrt ist. Dieses nur teilweise Erkennen des seitenverkehrten Bildes trägt natürlich dazu bei dass uns das Spiegelbild etwas eigenartig erscheinen mag.
Den Effekt des teilweisen Erkennens haben wir auch wenn wir ein Bild im Rückspiegel eines Autos betrachten. Wir registrieren wohl bei einem Auto hinter uns dass das Lenkrad auf der falschen Seite ist, wir registrieren aber nicht dass das ganze Bild seitenverkehrt ist. Denn wenn wir das Bild das wir im Rückspiegel sehen direkt sehen wollten so müssten wir uns ja um 180 Grad drehen wodurch ja aus unserer Sicht links und rechts des gesamten Bildes vertauscht wird. Dass das Spiegelbild als ganzes seitenverkehrt ist wird noch etwas deutlicher wenn man zu den beiden Männchen etwas „Umgebung“ dazu gibt wie es weiter unten in Bild 8 dargestellt ist.
Man könnte das Bild natürlich auch um die waagrechte Achse drehen wie im obigen Bild rechts (C) dargestellt ist. Geometrisch bewirkt das den gleichen Effekt, da wir aber nicht auf den Kopf gestellt herum laufen erscheint uns dieses Bild zwangsläufig unnatürlich. Hinzu kommt, dass wir nicht einmal dann ein auf den Kopf gestelltes sehen, wenn wir uns auf den Kopf stellen wollten. Das auf den Kopf gestellte Bild, das unsere Augen dann zweifelsfrei sehen wird automatisch in unserem Kopf korrigiert ohne dass wir irgend etwas davon merken.
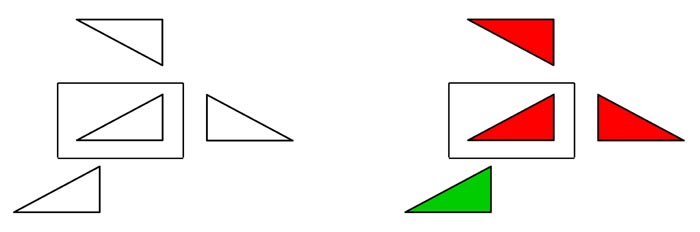
Wenn es sich um eine rein geometrische Figur handelt, wie ein Dreieck, oder einen Körper bei dem oben nicht festlegbar ist, dann erscheint uns übrigens auch bei Drehung um die horizontale Achse nichts unnatürlich. Das sieht man auch weiter unten an dem in Bild 9 dargestellten Körper. Bei einem solchen Körper registrieren wir übrigens auch nicht seitenverkehrt im Sinne von links-rechts.

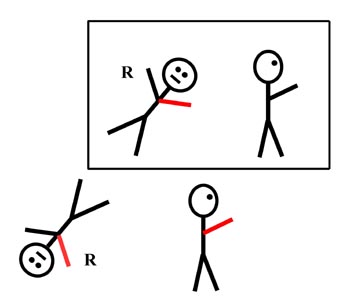
Wir stellen uns an einzelnen Objekten immer unbewusst jene Achse als seitenverkehrt vor wo wir eine links-rechts Symmetrie haben. Wenn wir uns etwa mit unserer rechten Seite zum Spiegel stellen so erscheint uns eben die Achse in Richtung Spiegel seitenverkehrt, was übrigens den tatsächlichen gespiegelten Richtung entspricht (Bild 2). Wenn wir uns etwa auf den Rücken legen wollten, so dass die Füße zum Spiegel schauen und der Kopf in die Gegenrichtung, so denken wir uns eben bezogen auf die umgedrehte Längsrichtung, wieder die Achse links-rechts als seitenverkehrt. In welcher Position wir uns auch immer zum Spiegel befinden, wir registrieren immer die links-rechts Achse als seitenverkehrt.

Bild 2

Dass man dies so sehen kann liegt daran, dass man bei einem dreidimensionalen spiegelbildlichen System jede der drei Achsen bezogen auf die anderen beiden Achsen, als seitenverkehrt ansehen kann. Dies kann man sich mit drei Fingern beider Hände, die man wie zwei Achsenkreuze spiegelbildlich zueinander hält, gut veranschaulichen. Dies ist weiter unten anhand von Bild 4 beschrieben.
Von diesem Umstand, dass man bei einem Spiegelbild jede beliebige Achse, bezogen auf die jeweils anderen beiden Achsen, als seitenverkehrt ansehen kann, machen wir eben unbewusst Gebrauch, wenn es sich um ein Objekt handelt bei dem links und rechts definierbar ist. Dies kann man sich wieder mit beiden Händen veranschaulichen, wenn man sie spiegelbildlich gegeneinander hält, wie es weiter unten anhand von Bild 5 beschrieben ist.

Wir registrieren also seitenverkehrt im Sinne von links-rechts nur dort wo es ein Objekt gibt für das wir eine linke und rechte Seite definieren können, wir registrieren aber nicht dass das gesamte Spiegelbild seitenverkehrt ist. Und wir registrieren schon gar nicht dass man ein Objekt im Spiegel bzw. das gesamte Spiegelbild in jede beliebige Richtung als seitenverkehrt ansehen kann.

Dass man ein Spiegelbild in jede beliebige Richtung als seitenverkehrt ansehen kann sieht man auch daran dass das Spiegelbild der Betrachtung eines Bildes von hinten entspricht, wie es weiter unten in Bild 7 dargestellt ist.
An einem Körper wo links-rechts nicht definierbar ist registrieren wir auch seitenverkehrt im Sinne von links-rechts nicht, was weiter unten anhand von Bild 9 beschrieben ist.

Damit ergibt sich als nächstes die Frage was links und rechts eigentlich genau bedeutet, wann genau erkennen wir bei einem Objekt links und rechts.

Vorher aber noch eine Anmerkung:
Mitunter wird behauptet dass wir links-rechts seitenverkehrt deshalb sehen weil wir uns selbst immer um die senkrechte Achse drehen. Das ist so nicht richtig, wir registrieren bei jeden Objekt bei dem links-rechts definierbar ist ein seitenverkehrtes Bild im Spiegel gleichviel in welcher Lage zum Spiegel sich das Objekt befindet.
Auf manchen Internetseiten wird behauptet dass hypothetische Männchen auf einem anderen Planeten, die sich immer auf den Kopf stellen würden wenn sie in die Gegenrichtung schauen wollten, im Spiegel Oben und Unten vertauscht sehen würden, also ein auf den Kopf gestelltes Männchen.
Das ist nun ein glatter Schwachsinn, im Spiegel ist ja deshalb alles seitenverkehrt weil ja in der Ebene des Spiegels alles dort bleibt wo es ist, nur dass eben vorne und hinten vertauscht wird. Tatsächlich kann man ein Spiegelbild in jede beliebige Richtung als seitenverkehrt ansehen.

Ein ebensolcher Schwachsinn ist es wenn in der Folge behauptet wird dass das Spiegelbild eine Frage der Psychologie sei. Das Spiegelbild ist ausschließlich eine Frage rein geometrischer Zusammenhänge. Wir haben allerdings von unserer Natur nur wenig Verständnis für die Geometrie des Spiegelbildes mitbekommen wohl weil es in der Natur keine Spiegel gibt.
Auch die Aussage dass das Spiegelbild durch Mathematik definiert ist und der Rest nur Phantasie sei ist glatter Unsinn. Selbstverständlich ist es interessant unter welchen Voraussetzungen wir seitenverkehrt im Sinne von links-rechts registrieren und es ist selbstverständlich rational nachvollziehbar.
============
Ein umgestülpter Handschuh

Spiegel in der Decke
=============

Gelegentlich besteht auch die Vorstellung dass wir wegen unserer zweier Augen spiegelbildlich sehen was auch nicht richtig ist.
Auch der Begriff des Spiegelparadoxons ist eher unzutreffend denn wenngleich wir von unserer Natur aus nur wenig natürliches Verständnis für die Geometrie des Spiegelbildes haben, so ist es doch rational durchaus erklärbar und hierfür ergibt der Begriff des Paradoxons keinen Sinn.

Damit zurück zur Frage was eigentlich links und rechts genau bedeutet, wie lässt sich links und rechts genau definieren.
Bei Lebewesen nehmen wir links und rechts wahr, bei einem Haus normalerweise nicht, bei einem Baum auch nicht, bei einem Auto aber schon. Wenn man, wie in einem Kinderbuch, einem Baum allerdings ein Gesicht aufmalen wollte so haben wir sofort links und rechts.
Dass man nämlich bei einem Lebewesen oder Gegenstand links und rechts überhaupt definieren kann setzt voraus das es zwei Achsen gibt die eine bestimmte Richtung haben, nämlich eine oben-unten Achse und eine vorne-hinten Achse, also dass Objekte in Richtung dieser beiden Achsen unsymmetrisch sind. Nur genau dann wenn sich für zwei Achsen eine bestimmte Richtung festlegen lässt, nämlich eine Achse nach oben und eine Achse nach vorne, also eine Unsymmetrie in Richtung dieser beiden Achsen besteht, dann kann man für die dritte Achse, die Querachse, bezogen auf die Lage der anderen beiden Achsen, links und rechts definieren. Eine der beiden Seiten ist dann links und die andere rechts, das muss man aufgrund einer Skizze festlegen (A im folgenden Bild), mit Worten kann man es nicht beschreiben wenn man nicht bereits weiß wo links und rechts sich befindet.

Bild 3

Etwas allgemeiner formuliert, wenn man einer ersten Achse eine Richtung zuordnet und einer zweiten Achse ebenfalls eine Richtung zuordnet, dann ist eine Seite der dritten Achse als links definiert und die andere Seite als rechts. Die Reihenfolge der ersten und zweiten Achse darf dabei nicht vertauscht werden sonst ändert sich auch links und rechts wie in im Bild oben in B. Das Achsenkreuz B entspräche z B. einem auf dem Rücken liegenden Menschen.
In Richtung dieser dritten Achse sind Lebewesen aber auch manche Gegenstände wie ein Auto zumeist einigermaßen symmetrisch. Das ist aber nicht unbedingt Voraussetzung denn Geräte wie etwa Baumaschinen oder etwa landwirtschaftliche Maschinen müssen durchaus nicht immer links-rechts symmetrisch sein, wenn aber oben und vorne eindeutig feststehen so kann man durchaus links und rechts eindeutig definieren. Eine leichte Unsymmetrie ist übrigens sogar erforderlich denn sonst könnte man zwischen links und rechts ja üpberhaupt keinen Unterschied erkennen.
Bei einer Lokomotive dagegen die in beide Richtungen fahren kann und in beide Richtungen gleich aussieht kann man links und rechts nicht angeben, man kann links und rechts nur bezogen auf die momentane Fahrtrichtung angeben. Wenn man freilich eine der beiden Richtungen der Lokomotive als vorne definiert, dann funktioniert auch links und rechts wieder.
Bei einem Baum kann man links und rechts nicht angeben, er hat ja auch kein vorne und hinten. Links und rechts könnte man hier allenfalls für die Richtung angeben aus der man den Baum gerade betrachtet was aber nicht viel Sinn ergibt.
Bei einem Haus könnte man etwa die Seite des Haupteingangs als vorne definieren und in der Folge auch links und rechts, das tun wir normalerweise aber nicht. Eher sprechen wir hier von einer Nord- und Südseite oder von einer West- und Ostseite.
Ein Schrank der im Zimmer steht hat sogar eindeutig oben und vorne, trotzdem sprechen wir hier normalerweise kaum von links und rechts.
Anscheinend haben wir weniger die Tendenz vorne und hinten zu registrieren wenn sich etwas nicht bewegt und daher beobachten wir bei solchen Gegenständen auch kaum links und rechts, auch nicht wenn es sich theoretisch definieren ließe.
Um also links und rechts definieren zu können erfordert das, dass es bei einem Objekt für zwei Achsen zwei ausgeprägte Richtungen, eine in Richtung oben und eine in Richtung vorne (Unsymmetrie in Richtung dieser Achsen), in bestimmter Lage zueinander gibt. Bei nicht bewegten Gegenständen registrieren wir allerdings vorne, und in der Folge links und rechts, weniger. Eine (näherungsweise) Symmetrie in der dritten Achse begünstigt dass wir links und rechts registrieren, ist aber nicht unbedingt Voraussetzung.
Vertauschen darf man die beiden Achsen aber auf keinen Fall. Dazu könnte man sich ein Auto, etwa einen Kombi mit senkrechter Rückwand, auf diese Rückwand gestellt vorstellen, so dass nun vorne oben ist. Wenn man nun die Vorderseite des Autos als oben definiert und das Dach als vorne, dann würden beim Auto links und rechts vertauscht.
Unser Achsensystem muss sich also immer mit dem Objekt mitbewegen, was wir uns ja auch automatisch vorstellen, sonst stimmt nichts mehr.
Hat man einmal eine oben Achse und eine vorne Achse für ein Lebewesen oder einen Gegenstand wie z.B. ein Auto festgelegt, was wir ohnehin automatisch tun, so ändert sich durch Bewegung in alle möglichen Richtungen nichts mehr wohin sich diese beiden Achsen nun mit dem Objekt auch immer mitbewegen.
Bei einem Kopfstand ist eben oben, oder man könnte auch sagen die erste Achse, unten und links und rechts entsprechen den mitgedrehten Achsensystem. Wenn sich jemand einmal auf allen Vieren bewegen wollte, so könnte man zwar wie bei Vierbeinern den Rücken als oben definieren und den Kopf als vorne. Allerdings heißt das dass oben zu vorne wird und hinten zu oben. Bei Vertauschen der beiden Achsen muss also auch die Richtung einer der beiden Achsen geändert werden damit links und rechts in gleicher Weise erhalten bleiben. Das ist aber unübersichtlich und daher auch nicht sinnvoll.

Damit noch einmal zurück zum Spiegel.
Wie gesagt, es muss bei einem Objekt links und rechts definierbar sein damit wir etwas seitenverkehrt im Spiegel registrieren.
Bei einem Schrank im Zimmer der durchaus oben und vorne aufweist nehmen wir seitenverkehrt im Spiegel schon kaum wahr, bei einer Zimmerpflanze, wo links und rechts nicht definierbar ist, noch weniger. Und dass man oben und und unten genau so als seitenverkehrt im Sinne von links-rechts ansehen kann nehmen wir schon gar nicht wahr man muss schon etwa seinen Kopf zur Seite neigen um dies feststellen zu können.

Man kann sich die Geometrie des Spiegelbildes gut mit seinen beiden Händen veranschaulichen.

Wie im folgenden Bild 4 dargestellt kann man mit jeweils drei Fingern beider Hände recht gut zwei dreidimensionale spiegelbildliche Achsenkreuze darstellen. Da die Finger nicht gerade Linien sind stellen sie ein Achsenkreuz natürlich nur näherungsweise dar, was aber für eine Veranschaulichung aber keine Rolle spielt.
Wenn man nun z.B. die beiden Zeigefinger beider Hände spiegelbildlich gegeneinander hält so erscheinen einem diese beiden Finger eben auch seitenverkehrt, während die beiden anderen Finger beider Hände in die gleiche Richtung zeigen. Den gleichen Eindruck hat man wenn man Mittelfinger oder Daumen spiegelbildlich gegeneinander hält. Man sieht immer jenes Fingerpaar als seitenverkehrt dass man tatsächlich spiegelbildlich gegeneinander hält, während die beiden anderen Finger in die gleiche Richtung zeigen. Das heißt aber natürlich auch dass man bei einem dreidimensionalen Achsenkreuz jede der drei Richtungen, in dem Fall Fingerpaare, als seitenverkehrt gegenüber den anderen beiden Richtungen, in dem Fall gegen die anderen beiden Fingerpaare, ansehen kann. Denn an der Geometrie der Finger ändert sich ja nichts dadurch dass man sie anders hält
Man sieht daran also dass man bei einem spiegelbildlichen Achsenkreuz jede der drei Richtungen, bezogen auf die anderen beiden Richtungen als seitenverkehrt ansehen kann.
Wenn man übrigens die Finger beider Hände beliebig schräg, aber spiegelbildlich, zueinander hält so sieht man zwei oder auch alle drei Fingerpaare als seitenverkehrt zueinander. Bei einem Objekt wo seitenverkehrt im Sinne links-rechts nicht definierbar ist, wie das bei einem mit den Fingern dargestellte Achsenkreuz der Fall ist, dann sehen wir immer jene Richtung als seitenverkehrt die momentan auch tatsächlich spiegelbildlich ist. Das sieht man übrigens auch beim Körper in Bild 9.

Bild 4

Genau von der Möglichkeit, bei einem spiegelbildlichen System jede beliebige Richtung als seitenverkehrt ansehen zu können, machen wir bei Objekten bei denen eine links-rechts Achse definierbar ist, unbewusst Gebrauch. Man kann sich dies wie im folgenden Bild 5 dargestellt gut mit seinen beiden Händen veranschaulichen.
Wie immer man beide Hände spiegelbildlich zueinander hält, wir registrieren immer die Richtung quer zu den Fingern als seitenverkehrt. Wir sehen zwar dass im folgenden Bild die beiden Hände in Längsrichtung spiegelbildlich sind, nur registrieren wir trotzdem die Querrichtung zu den Fingern als seitenverkehrt. Wir registrieren also jene Achse als seitenverkehrt, wo im Gegensatz zu anderen beiden Achsen eine (grob) näherungsweise Symmetrie besteht. Oder andersherum betrachtet wir verwenden jene beiden Achsen, wo definitive Unsymmetrie besteht (Längsrichtung der Finger, Handfläche-Handrücken) als Bezugsachsen und registrieren jene Achse wo näherungsweise Symmetrie besteht (Querrichtung zu den Fingern) im Verhältnis dazu als seitenverkehrt.
Diese Sichtweise steht in direkten Gegensatz zum Achsenkreuz vorher wo wir immer die aktuell gespiegelte Richtung als seitenverkehrt registrieren.

Die Hände sind zwar kein ideales Beispiel aber wir haben sie "zur Hand" und es funktioniert zur Veranschaulichung durchaus. Die Hände sind in zwei Richtungen, in Längsrichtung der Finger und in Richtung Handfläche-Handrücken ausdrücklich unsymmetrisch und sie sind quer zu den Fingern immerhin grob symmetrisch. Man könnte zwar die Finger als oben ansehen und die Handfläche als vorne, eindeutig ist das aber nicht. Insofern ist auch nicht definitiv festlegbar welche Seite einer Hand man als links und als rechts ansehen will. Wohl aber ist, wie gesagt, eine Hand in zwei Richtungen ausdrücklich unsymmetrisch während sie in die dritte Richtung immerhin grob symmetrisch ist. Das reicht offensichtlich auch dass wir die beiden Hände immer quer zu den Fingern, also die Richtung in der die Hände grob symmetrisch sind, als seitenverkehrt ansehen.
An dieser Sichtweise ist natürlich nichts falsch, es geschieht aber unbewusst und es mag einem, wenn man es bewusst nachvollzieht, als etwas "willkürlich" erscheinen.

Bild 5

Das gleiche geschieht auch wenn wir ein Objekt im Spiegel betrachten bei dem eine links-rechts Achse definierbar ist.
Wir verwenden unbewusst immer jene beiden Achsen in der ein Objekt unsymmetrisch ist (oben-unten, vorne-hinten) als Bezugsachsen, während wir die näherungsweise symmetrische Achse (links-rechts) als seitenverkehrt dazu registrieren. Oder man könnte auch sagen, wir nehmen die oben-unten Achse und die vorne-hinten Achse immer als "richtig" an während wir die links-rechts Achse im Verhältnis dazu als "falsch" also als seitenverkehrt sehen. Dabei ist es völlig gleichgültig in welcher Lage sich ein Objekt oder wir selbst uns zum Spiegel befinden, ob wir etwa mit der linken Seite zum Spiegel stehen oder uns etwa mit den Füßen in Richtung Spiegel legen wollten.

Wenn wir den Kopf nach links verdrehen so erscheint er im Spiegel nach rechts verdreht. Wenn wir es aber aus Sicht unseres Kopfes betrachten so ist der Rücken auf der linken Seite unseres Kopfes, im Spiegel ist es umgekehrt.
Wenn wir den Kopf nach links neigen so erscheint er im Spiegel nach rechts geneigt. Aus Sicht unseres Kopfes ist unser Körper auf der linken Seite unseres Kopfes, im Spiegel ist es umgekehrt.
Wir verwenden also selbst an einem Objekt, hier an uns selbst, ohne weiteres zwei verschiedene Bezugssysteme ohne dass uns dies in irgend einer Weise bewusst wäre.

Bei Objekten wo seitenverkehrt im Sinne von links-rechts nicht definierbar ist sehen wir immer jene Richtung als seitenverkehrt die der tatsächlichen momentanen Spiegelung entspricht.
Dagegen registrieren wir bei Objekten bei denen eine Richtung als links-rechts definierbar ist, immer in Richtung von links-rechts als seitenverkehrt, ganz gleich in welcher Richtung das Objekt auch momentan gespiegelt ist. Beides ist gleich richtig wenngleich einem letzteres als etwas willkürlich erscheinen mag.

Ein weiteres interessantes Beispiel für seitenverkehrtes Sehen sind Buchstaben und Ziffern. Der Buchstabe "R" z.B. ist in Richtung links-rechts genauso unsymmetrisch wie in Richtung oben-unten. Insofern könnte man den Buchstaben "R" in der oben-unten Achse genau so gut als seitenverkehrt ansehen wie in der Querachse. Gäbe es einen Buchstaben der wie ein liegendes "R" aussieht, so würde man diesen Buchstaben genauso als links-rechts seitenverkehrt ansehen.
Allerdings wissen wir wo beim Buchstaben "R" oben ist und haben damit eine Bezugsachse, wie bei den Männchen im Spiegel auch. Und wir wissen auch wie der Buchstabe links und rechts aussehen muss, jedenfalls wenn wir von vorne auf das Papier sehen. Damit registrieren wir das "R" im Spiegel immer quer zur Hochachse als seitenverkehrt. Hier geht also die Richtung die wir als seitenverkehrt ansehen nicht aus der Symmetrie bzw. Unsymmetrie der verschiedenen Achsen hervor, sondern daraus dass wir wissen wo bei diesen Buchstaben oben ist und wie links und rechts aussehen muss.
Man sieht übrigens das spiegelbildliche eines Buchstabens noch deutlicher wenn er Teil eines Wortes es ist.
Bei genauer Betrachtung sind also die Gründe dafür dass wir etwas als links-recht seitenverkehrt registrieren nicht völlig identisch, wenngleich es auf dem gleichen Prinzip beruht.

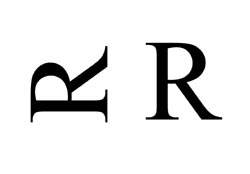
Bild 6

Noch etwas anders verhält es sich bei Türen. Ein Türblatt ist meistens weder in Richtung oben-unten noch in Richtung vorne-hinten sonderlich unsymmetrisch. Allerdings wissen wir natürlich wo oben ist wenn wir vor einer Tür stehen. In diesem Fall hat man es so festgelegt dass eine Tür als links angeschlagen gilt, wenn unter der Voraussetzung dass sich die Tür auf der gleichen Seite der Mauer befindet auf der man selbst steht bzw. sich die Tür zu einem her öffnet, die Türangel aus dieser Sicht links ist. Diese Festlegung ist plausibel aber im Prinzip willkürlich.
Normalerweise registrieren wir nicht auf welcher Seite eine Tür angeschlagen ist und wir registrieren normalerweise auch im Spiegel nicht dass eine Tür seitenverkehrt ist. Nur wenn wir es bewusst betrachten sehen wir im Spiegelbild eine Tür auch als Links-Rechts seitenverkehrt.

Ähnlich verhält es sich bei einem Schrank. Ein Schrank hat eindeutig ein Vorne und Oben, Links-Rechts ist daher eindeutig definierbar. Wir registrieren dies aber normalerweise nicht, unabhängig davon ob der Schrank nun einigermaßen Links-Rechts symmetrisch ist oder auch nicht. Wir registrieren auch im Spiegelbild einen Schrank normalerweise nicht als seitenverkehrt. Nur wenn wir bewusst das Spiegelbild vergleichen registrieren wir auch hier wieder die Links-Rechts Achse als seitenverkehrt.

Wenn man sich fragt, warum wir ein Auto sofort als seitenverkehrt im Spiegel registrieren, eine Tür oder einem Schrank aber nicht, so hat das wohl damit zu tun dass ein Auto dass Lenkrad immer auf der linken Seite hat.
Wären alle Türen links angeschlagen so würde uns wahrscheinlich auch im Spiegel auffallen, dass die Türen im Spiegel auf der anderen Seite angeschlagen sind. Hätten alle Schränke z.B. auf der linken Seite eine Lade, so würde uns wahrscheinlich auch hier auffallen dass die Lade im Spiegel auf der falschen Seite ist.
Hätten umgekehrt Autos regellos auf beiden Seiten das Lenkrad, so würde uns wahrscheinlich auch im Spiegel kaum auffallen dass sie seitenverkehrt sind.
Hinzu kommt dass bei unbewegten Gegenständen wie Schränken Links und Rechts im Alltag auch praktisch keine Bedeutung hat.
Zu sagen ist noch dass wir auch hier, sofern wir es überhaupt registrieren, seitenverkehrt immer in der Links-Rechts Achse sehen, niemals in der Oben-Unten Achse oder in der Vorne-Hinten Achse.

Noch etwas anders verhält es sich bei einem Haus. Links und Rechts sind hier nicht wirklich definiert, es sei denn man legt etwa die Seite des Haupteingangs als Vorne fest. Jedenfalls registrieren wir hier praktisch niemals Links und Rechts und wir registrieren normalerweise auch im Spiegelbild ein Haus nicht als seitenverkehrt. Wenn wir es aber wieder bewusst beobachten, so registrieren wir die horizontale Richtung eines Hauses als seitenverkehrt, eigentlich unabhängig davon welche Seite des Hauses wir im Spiegel gerade sehen.

Bei einem Baum ist Links und Rechts nicht definierbar und wir registrieren ihn im Spiegel auch nicht als seitenverkehrt. Wenn wir es aber bewusst beobachten so registrieren wir auch hier wieder die Querrichtung des Baumes im Spiegelbild als seitenverkehrt. Das ist jene Richtung die bei uns selbst im Spiegel meist die Links-Rechts Richtung ist und wo wir uns daher normalerweise im Spiegel auch als seitenverkehrt registrieren.

Noch eine Anmerkung:
Damit wir etwas als seitenverkehrt sehen ist in der betreffenden Achse zumindest eine gewisse Unsymmetrie notwendig, denn wenn ein Objekt in eine Richtung völlig symmetrisch ist kann man diese Richtung ja auch nicht als seitenverkehrt registrieren.
Ein Auto ist weitgehend symmetrisch, es hat aber nur auf einer Seite ein Lenkrad. Ein Auto registrieren wir daher sofort als seitenverkehrt im Spiegelbild.
Wir selbst sind weitgehend Links-Rechts symmetrisch und wir sehen ja auch nur unser Spiegelbild und nicht uns selbst. Bei uns selbst fällt uns daher seitenverkehrt hauptsächlich durch Bewegung auf, rein am Spiegelbild selbst würden wir seitenverkehrt wohl nicht unbedingt registrieren. Bei einer eindeutigen Unsymmetrie, sei es Bekleidung, sei es z.B. eine Narbe registrieren wir dagegen seitenverkehrt viel eher auch ohne irgend eine Bewegung.

Ein etwas anderes Beispiel:
Wenn ich einen Abdruck von meiner Handfläche auf Papier mache dann passt dieser Abdruck genau so lange, so lange ich mir vorstelle dass der Handrücken beim Abdruck mir selbst zugewandt ist. Sobald ich mir aber vorstelle dass mein Handrücken auf der anderen Seite des Papiers ist, ich mir den Abdruck also so vorstelle als ob ich mir meine Handfläche ansehen wollte, dann ist der Abdruck meiner Handfläche seitenverkehrt. Um meine Handfläche sehen zu können muss ich ja meine Hand um eine Achse um 180 Grad drehen, was beim Abdruck der Handfläche auf das Papier nicht geschieht. Die Hand kann man um jede beliebige Achse zurückdrehen wenn man die Handfläche richtig sehen will und der Abdruck auf Papier ist immer seitenverkehrt dazu, ganz gleich ob die Finger beim Abdruck nach oben zeigen oder in sonst eine Richtung.
Man kann auch sehen dass beim Abdruck der Handfläche der rechten Hand der Daumen im Uhrzeigersinn immer hinter den anderen Fingern ist, gleichviel in welche Richtung die Finger auch immer zeigen, während beim direkten Betrachten der rechten Handfläche der Daumen im Uhrzeigersinn immer vor den Fingern ist.
Das mag selbstverständlich erscheinen, es zeigt aber dass eine Drehung um jede beliebige Achse das gleiche seitenverkehrte Bild ergibt und zeigt damit auch dass zu jedem Bild genau nur ein seitenverkehrtes Bild existiert.
Denselben Effekt haben wir im Spiegel. Wenn wir unsere Handfläche im Spiegel ansehen dann haben wir eben den Eindruck als ob die Hand um 180 Grad gedreht wäre und damit ist das Bild in der Tat seitenverkehrt.

Im folgenden Bild sind links noch einmal die beiden Männchen dargestellt. Daneben vor dem Spiegel steht ein Foto der beiden Männchen von vorne das auf durchsichtigen Papier gedruckt ist. Das Foto von hinten betrachtet ergibt das gleiche Bild wie das Spiegelbild. Ein auf Glas gemaltes Bild das man von der Rückseite betrachtet entspricht also dem Spiegelbild dieses Bildes.
Auch daran sieht man eindeutig dass einem bestimmten Bild genau ein Spiegelbild entspricht und ein Spiegelbild daher in jede beliebige Richtung, im Sinne von links-rechts, als seitenverkehrt ansehen kann. Man kann das Bild schließlich um jede beliebige Achse zurückdrehen und das Bild erscheint dann immer um eine andere Achse gespiegelt zum Spiegelbild. Man sieht das eigentlich auch in Bild 1 in B und C.

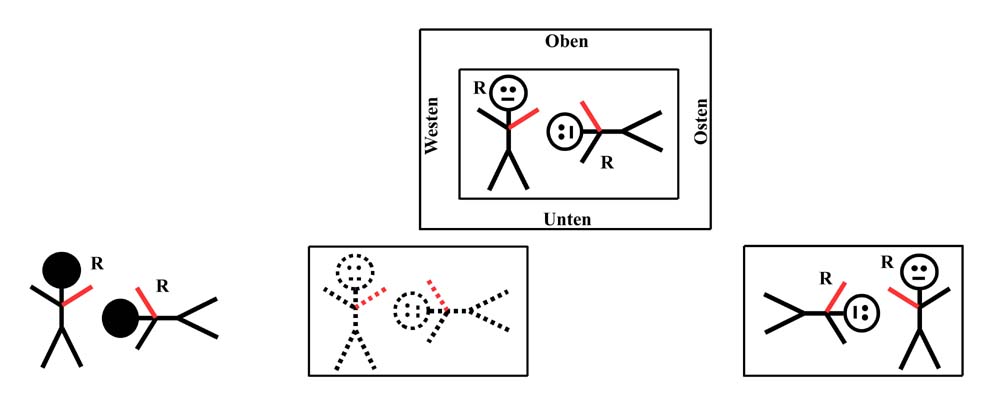
Bild 7

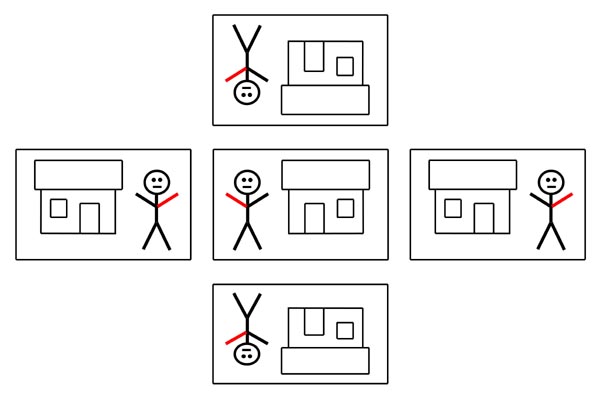
Als nächstes sind die beiden Männchen mit etwas „Landschaft“ dargestellt.
Man sieht hier sehr gut dass wir im Spiegel zwar registrieren dass die beiden Männchen seitenverkehrt sind, die müssten nämlich, jedes für sich, so aussehen wie sie rechts neben dem Spiegel (A) dargestellt sind. Bei dem Baum dagegen registrieren wir dass er auf der richtigen Seite im Sinne von Westen und Osten ist, wir registrieren jedoch nicht dass das Bild im Spiegel als Ganzes einschließlich des Baumes seitenverkehrt ist.
Denn, wollte man wieder ein Foto der Männchen mit Landschaft von vorne machen so würde es so aussehen wie es unten rechts (B) dargestellt ist. Denn wenn wir die Männchen von vorne sehen wollten dann müssten wir uns ja um die eigene Achse drehen womit links und rechts des gesamten Bildes vertauscht würde.
Denselben Effekt haben wir, wie gesagt auch wenn wir ein Auto im Rückspiegel sehen. Beim Auto registrieren wir dass es seitenverkehrt ist, nicht aber bei dessen Umgebung.

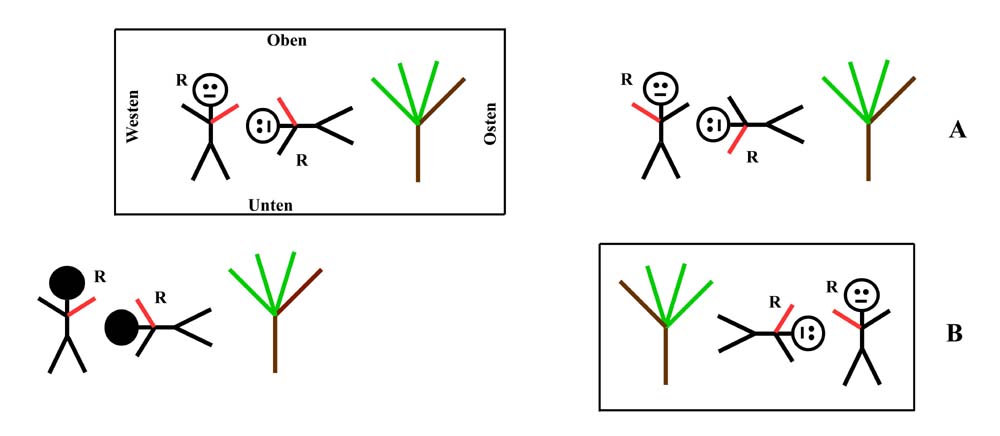
Bild 8

Im folgenden noch eine andere grafische Darstellung, die das Dreidimensionale betrachtet.
Im folgenden Bild 9 ist links ein Körper (A) mit seinem Spiegelbild dargestellt. Rechts davon ist der gleiche Körper um die senkrechte Achse nach hinten gedreht (B), oben über dem Spiegel ist er um die waagrechte Achse nach hinten gedreht (C) dargestellt. Man sieht hier gut dass das Bild im Spiegel immer der Spiegelung des Körpers, nur um eine andere Achse entspricht.
In einem Spiegel (D), wie mit der strichlierten Linie angedeutet, würde man den Körper von rechts betrachtet (B) gleich sehen wie den Körper im Spiegel von vorne betrachtet (A). Analoges gilt wenn man den Körper von oben (C) in einem Spiegel (E) betrachtet.
Man sieht daraus dass dass die Spiegelung eines Körpers immer den gleichen gespiegelten Körper ergibt, ganz gleichgültig zu welcher Ebene man sich den Körper gespiegelt vorstellen will. Zu einem Körper gibt es also genau einen spiegelbildlichen Körper. Das kann man sich aber auch mit seinen beiden Händen gut vergegenwärtigen (Bild 5). Umgekehrt betrachtet, wenn man das Spiegelbild als Körper ansieht, kann man hier natürlich auch sehen dass eine Spiegelung eines Körpers um jede beliebige Achse gespiegelt den gleichen Körper ergibt, wenn auch um eine Achse gedreht ist.
Bei einem Körper der kein ausdrückliches oben und unten hat erscheint uns übrigens die Drehung um die waagrechte Achse genau so natürlich wie die Drehung um die senkrechte Achse, es erscheint hier nichts auf den Kopf gestellt.
Bei einem Körper bei dem links und rechts nicht definierbar ist registrieren wir seitenverkehrt im Sinne von links-rechts auch nicht. Würde man dagegen auf eine der Flächen des Körpers ein Gesicht zeichnen, so würden wir an diesen Gesicht sofort links-rechts seitenverkehrt registrieren, vorausgesetzt allerdings dass das Gesicht nicht vollständig symmetrisch ist.
Bei einem solchen Körper registriert man auch viel eher dass in einem Spiegel vorne mit hinten vertauscht erscheint.

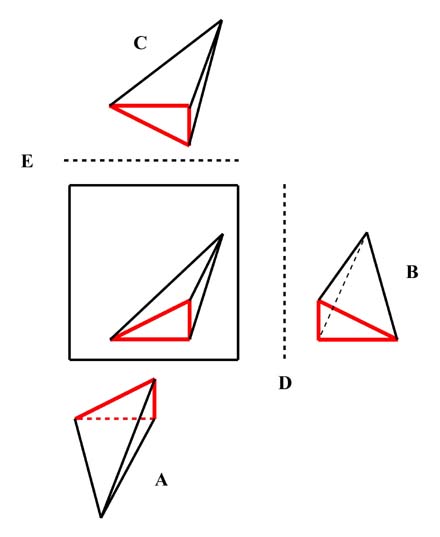
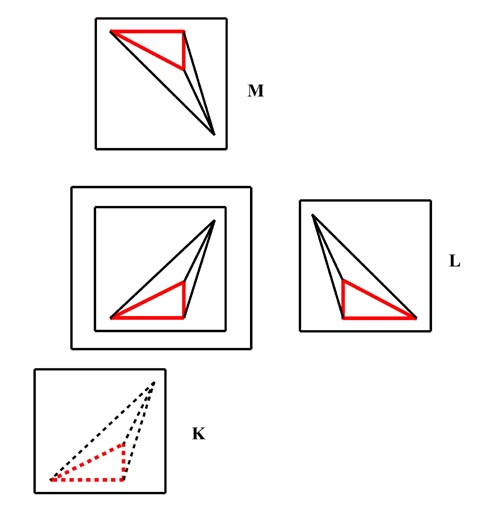
Bild 9

Am vorherigen Bild (links) sieht man also:
Seitenverkehrt im Sinne von links-rechts registrieren wir in einem Spiegelbild nur dann, wenn es sich um einen Körper handelt für den links-rechts auch definierbar ist.
An einer Drehung um die waagrechte Achse (Vertauschen von oben und unten) erscheint uns nichts unnatürlich wenn bei einem Körper kein Oben-Unten definierbar ist.
Zu jedem Körper gibt es genau einen spiegelbildlichen Körper, ganz gleich um welche Ebene man den Körper spiegelt.

Im Bild 9 ist rechts noch ein ein interessanter Nebeneffekt dargestellt. Auf der linken Seite werden die Körper und das Spiegelbild immer aus der gleichen Perspektive, von vorne oben rechts, angesehen. Da der Körper gedreht wird ergibt das in der zweidimensionalen Projektion immer eine andere zweidimensionale Geometrie.

Auf der rechten Seite ist der Körper dagegen bereits als zweidimensionales Bild dargestellt, auf durchscheinenden Papier von hinten gesehen (K), das Bild um die senkrechte Achse gedreht (L) und um die waagrechte Achse gedreht (M). Hier wandert die Perspektive zwangsläufig bei Drehung des Bildes mit, in L erscheint das Bild von vorne links oben gesehen, in M erscheint es von vorne rechts unten gesehen. Die Projektion des Körpers auf das zweidimensionale erscheint daher immer als die gleiche Geometrie, wenngleich immer um eine Achse gedreht, also in spiegelbildlicher Form. Das ist ein kleiner aber doch interessanter Nebeneffekt.

Hier noch ein Vergleich von zweidimensionaler Geometrie mit dreidimensionaler Geometrie.
Die Handflächen beider Hände passen immer aufeinander. Man kann die beiden Handflächen zwar beliebig spiegelbildlich halten, aber man kann sie immer so drehen dass die Handflächen aufeinander passen. Mit den ganzen Händen, die Hände als dreidimensionaler Körper betrachtet, geht dass nicht, sie sind immer spiegelbildlich zueinander.
Im folgenden Bild 10 ist das anhand eines Dreieckes dargestellt. Solange man das Dreieck als rein zweidimensionale Geometrie betrachtet, etwa aus Papier ausgeschnitten ohne die zwei Seiten des Papiers zu unterscheiden, kann man das Dreieck immer so drehen dass es seinem Spiegelbild bzw. einem spiegelbildlichen Dreieck entspricht. Rein zweidimensional betrachtet gibt es also nicht wirklich eine spiegelbildliche Geometrie, es ist eigentlich die gleiche Geometrie, nur in eine andere Position gedreht.
Sobald man aber dem Dreieck auf beiden Seiten zwei unterschiedliche Farben gibt kann man es nicht mehr so drehen dass es dem Spiegelbild bzw. einem spiegelbildlichen Dreieck entspricht. Zwei dreidimensionale spiegelbildliche Geometrien und seien es nur die unterschiedlichen Farben beider Seiten, sind immer spiegelbildlich zueinander, wie man sie auch immer dreht und wendet. Auch die beiden Hände sind, wie gesagt, immer spiegelbildlich zueinander. Wenn man sie überhaupt nicht spiegelbildlich zueinander hält, also die eine Hand senkrecht und die andere waagrecht, dann ändert dass an der spiegelbildlichen Geometrie auch nichts, man registriert es nur nicht unmittelbar.

Bild 10

Die einzelnen Flächen eines spiegelbildlichen Körpers für sich genommen sind aber wieder alle gleich. Im vorherigen Körper (Bild 9) entsprechen alle Dreiecke der Oberflächen beider Körper einander, wie eben etwa die Handflächen beider Hände auch aufeinander passen.
Wollte man allerdings die beiden spiegelbildlichen Körper aus völlig identischen zweifarbigen Dreiecken zusammensetzen, die etwa auf der einen Seite rot sind und auf der anderen Seite grün, so wäre einer der beiden Körper rot der andere grün. Denn um eine spiegelbildlichen Körper zu erhalten müsste jeweils die andere Seite der einzelnen Flächen außen sein.

Nebenbemerkung.
Dass wir in einen Spiegel so gut räumlich sehen hat auch einen Grund. Das Licht das von einem Bildpunkt ausgeht und bei den beiden Augen eintrifft wird auch am Spiegel an zwei verschiedenen Stellen reflektiert, beide Augen sehen einen Bildpunkt auf der Spiegeloberfläche an einen geringfügig anderen Ort. Das heißt der Effekt zweier geringfügig unterschiedlicher Bilder für beide Augen ist auch am Spiegel erfüllt. Das ist bei einem zweidimensionalen Bild auf Papier oder am Bildschirm nicht der Fall, wir sehen in diesen Fall auch kein räumliches Bild.
Dass sich das Spiegelbild ändert je nachdem aus welcher Richtung wir in den Spiegel sehen, man sieht in den Spiegel so als ob man durch ein Fenster sehen würde, mag zu diesen Eindruck beitragen, es ist aber nicht die Ursache für das räumliche Sehen.

Analog wie beim Spiegelbild verhält es sich übrigens auch wenn man ein Foto spiegeln will.
Ganz gleich um welche Achse man ein Bild spiegelt, es kommt immer das gleiche gespiegelte Bild heraus, wenn auch in eine unterschiedliche Richtung gedreht. Dies erwartet man sich zunächst vielleicht nicht unbedingt. Aber im Prinzip ist die Spiegelung eines Fotos zu einer Achse das gleiche wie wenn man sich vorstellt dass man ein auf Glas gedrucktes Bild um eine Achse dreht, so dass man das Bild von der anderen Seite sieht. Dann ist einem sofort klar dass es das gleiche Bild sein muss. Rein zweidimensional betrachtet kann man es auch hier sogar als das gleiche Bild ansehen nur eben um eine Achse gedreht.

Bild 11

Man kann das Bild natürlich um jede beliebige Achse spiegeln, so wie man ein Bild auf Glas ja auch um jede beliebige Achse drehen kann. Bei der Spiegelung um eine Achse die um 45 Grad gedreht ist, wie es im folgenden Bild auf der linken Seite dargestellt ist, erkennt man nicht unbedingt gleich dass es sich um gespiegelte Bilder handelt. Wenn man sich aber die beiden Bilder gemeinsam um 45 Grad gedreht vorstellt, wie rechts im folgenden Bild dargestellt, dann sieht man sofort dass es sich um zwei zueinander gespiegelte Bilder handelt.

Bild 12

Nebstbei, im vorherigen Bild sieht man auch eine optische Täuschung. Das Hochformat scheint andere Proportionen zu haben als das Querformat. Die rechten Bilder erscheinen sogar noch etwas größer, wohl weil die Diagonale näherungsweise senkrecht ist. Tatsächlich sind alle vier Rechtecke, die die Fotos darstellen, gleich groß und ihre Proportionen, Länge zu Breite, sind auch gleich.

Am Ende könnte man sich noch fragen warum wir für links und rechts doch ein einigermaßen natürliches Verständnis entwickelt haben, auch wenn man es sich überlegen muss was es eigentlich genau heißt, wir aber für die seitenverkehrte Ansicht in einem Spiegels viel weniger ein natürliches Verständnis entwickelt haben.
Nun die seitenverkehrte Ansicht in einem Spiegel ist schon tatsächlich etwas komplizierter, es liegt aber wohl daran dass Spiegel in der Natur praktisch nicht vorkommen. Spiegel gibt erst seit einigen tausend Jahren und dass sie allgemein verfügbar sind liegt noch viel kürzer zurück und das ist in der Evolution eine sehr kurze Zeit. Es ist wohl bei weitem zu kurz als dass wir dafür ein ähnlich natürliches Verständnis entwickelt hätten als wie wir das bei links und rechts bei realen Körpern doch einigermaßen automatisch empfinden.

Verwandte Themen:

Räumliches Sehen

Optische Täuschung beim bekannten Wasserfall

Farbe sehen und Farbmodelle

Startseite